Sine 60 Degrees Exact Value

In trigonometry, in that location are three major or primary ratios, Sine, Cosine and Tangent, which are used to find the angles and length of the right-angled triangle. Earlier discussing Sin threescore degrees, let u.s.a. know the importance of Sine function in trigonometry. Sine function defines a relation between the angle(formed between the hypotenuse and adjacent side) and the opposite side to the angle and hypotenuse. Or you can say, the Sine of bending theta is equal to the ratio of perpendicular and hypotenuse of a right-angled triangle.

The trigonometry ratios sin, cos and tan for an angle are the main functions. The value of sin 60 degrees and other trigonometry ratios for all the degrees 0°, 30°, 45°, ninety°,180° are by and large used in trigonometry equations. These values are like shooting fish in a barrel to memorize with the assist trigonometry table. Let us discuss the value of sine 60 degrees hither in this article.

Besides, read:

• Sine Office
• Sin 0 Degree
• Sin thirty Degrees
• Sin 45 Degrees
• Sin 90 Degrees
• Constabulary of Sines

Value of Sin 60 Degree

In a right-angled triangle, the sine of angle α is a ratio of the length of the contrary side(perpendicular) to the length of the hypotenuse side.

Sin α= Opposite Side/Hypotenuse

=Perpendicular Side/Hypotenuse Side

= a/h

And so, the ratio sin 60 degrees role will exist, sin 60 = Perpendicular/Hypotenuse

In that location is a unproblematic method by ways of which nosotros can calculate the value of sine ratios for all the degrees. If yous learn this method, you can hands calculate the values for all other trigonometry ratios. So, allow'south showtime with calculating the values for sin 0°, sin thirty°, sin 45°, sin 60°, sin ninety°.

Sin 0°=

\(\begin{assortment}{l}\sqrt{0/4}\end{assortment} \)

= 0

Sin 30°=

\(\begin{assortment}{l}\sqrt{1/4}\end{array} \)

= ½

Sin 45°=

\(\begin{array}{l}\sqrt{2/4}\end{array} \)

= 1/√ii

Sin sixty°=

\(\begin{array}{l}\sqrt{iii/4}\stop{assortment} \)

= √iii/2

Sin 90°=

\(\begin{array}{l}\sqrt{4/4}\stop{array} \)

= ane

From the to a higher place equations, we get sin 60 degrees exact value as √3/2. In the aforementioned way, we tin can discover the values for cos and tan ratios.

Therefore, the exact value of sin sixty degrees is √3/two

Cos 0° = Sin ninety°= 1

Cos 30°= Sin lx°= √iii/2

Cos 45°= Sin 45°= 1/√2

Cos 60°= Sin 30° =1/2

Cos 90° = Sin 0°= 0

As well,

Tan 0°= Sin 0°/Cos 0°= 0

Tan 30°= Sin thirty°/Cos 30°=one/√iii

Tan 45°= Sin 45°/Cos 45°= 1

Tan 60°= Sin threescore°/Cos 60°= √3

Tan 90°= Sin 90°/Cos 90°= ∞

The above values of trigonometry ratios are with respect to degrees. We tin can also mention the values with respect to radians. Radians is considered for unit of measurement circle, whose radius is equal to one. The radian is denoted by π.

For 0°, the value of radian is 0. In the aforementioned mode, we tin create a table for trigonometry ratios with respect to π.

Radian	0	π/6	π/4	π/3	π/2	π	3π/2	2π
Sin	0	1/2	\(\begin{array}{l}ane/\sqrt{2}\cease{assortment} \)	\(\begin{assortment}{l}\sqrt{iii}/ii\end{array} \)	ane	0	-1	0
Cos	1	\(\begin{array}{l}\sqrt{3}/2\cease{array} \)	\(\begin{array}{50}i/\sqrt{2}\end{array} \)	1/ii	0	-1	0	1
Tan	0	1/ \(\begin{array}{l}\sqrt{3}\finish{array} \)	1	\(\begin{array}{50}\sqrt{3}\end{array} \)	Undefined	0	Undefined	0

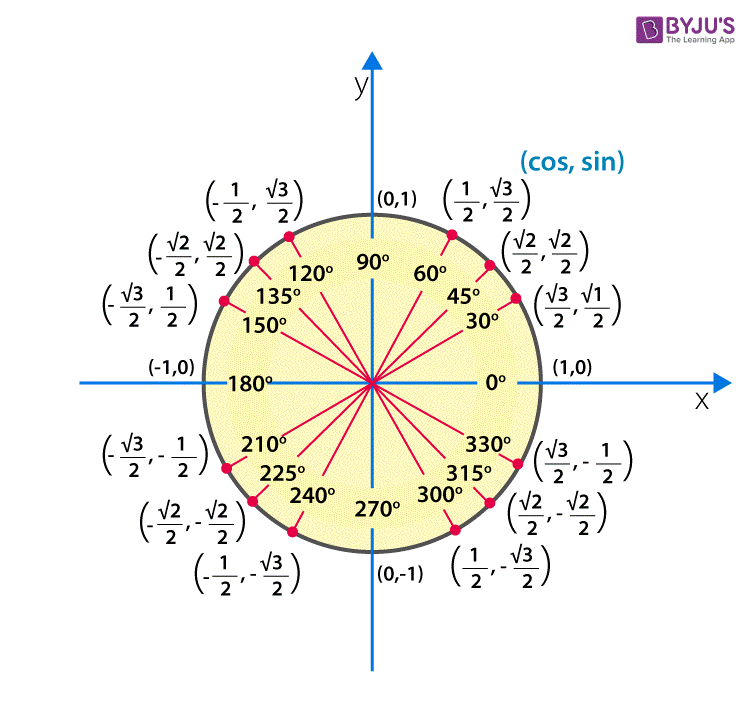
We learned about sin threescore degrees value forth with other degree values hither, this far. Also, derived the value for cos degree and tan degrees with respect sin degrees and also in terms of radians. In the same way, we can find the values for other trigonometric ratios like sec, cosec and cot.

Acquire more than about trigonometric ratios and identities and download BYJU'South-The Learning App for a better experience.

Sine 60 Degrees Exact Value,

Source: https://byjus.com/maths/sin-60-degrees/#:~:text=From%20the%20above%20equations%2C%20we,value%20as%20%E2%88%9A3%2F2.

Posted by: funketingettere.blogspot.com

Share this post